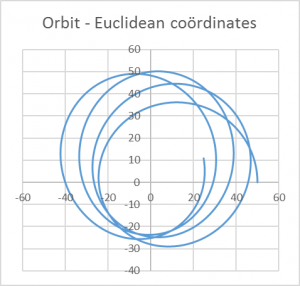
Simulating an orbit around a spherical mass
The curvature of space-time around a spherical mass is described by the Schwarzschild metric.
We provide an Excel file simulating the orbit of a test particle around the spherical mass using a straightforward forward Euler simulation.
Download link: 20161106_geodesic_line_simulation_riemann_schwarzschild_2d_v3
The simulation is performed in a 2-dimensional space where
or
![Rendered by QuickLaTeX.com d\tau^2 = \left[ \begin{matrix} dr & d \varphi & dt \end{matrix} \right] \left[ \begin{matrix} - \left(1 - \frac{2GM}{r}\right)^{-1} & 0 & 0 \\ 0 & - r^2 & 0 \\ 0 & 0 & \left(1 - \frac{2GM}{r}\right) \end{matrix} \right] \left[ \begin{matrix} dr \\ d \varphi \\ dt \end{matrix} \right] = g_{ij} dx^i dx^j](https://ivan.goethals-jacobs.be/wp-content/ql-cache/quicklatex.com-1f57e1d3b974797a6d315e3b7f1a6908_l3.png)
where the right hand side uses Einstein notation.
Given coördinates ![]() and first order derivatives
and first order derivatives ![]() at time
at time ![]() , the 2nd order derivatives feeding the simulation can be derived using the geodesic equation:
, the 2nd order derivatives feeding the simulation can be derived using the geodesic equation:
where
again using Einstein notation and with
The exact matrices
An example is provided below and can be simulated in the Excel by setting the starting values to ![]() and
and ![]() and the simulation step size to
and the simulation step size to ![]() .
.